Twenty-Sided Die Game

In this blog post we are going to discuss a mock quantitative interview question by Jane Street. Suppose you are offered to play the following game: at the start of the game a twenty-sided die is rolled. At the start of each round of the game you are given a choice to either take money in the amount equal to the face of the die that is currently up or roll the die. If you choose to roll the die, you forfeit the opportunity to take money in this round. If the die is not rolled in a given round, the state of the die is transfered to the next round. The game lasts for 100 rounds. Your goal is to come up with a strategy to maximize the total amount of money received.

Strategy of Never Rolling

We will start our analysis by considering a strategy of never rolling the die and always taking money starting from round one. For example, if the die has been rolled to return a value of one at the beginning of the game, our return will just be equal to $ \$1\times 100=\$100$. This is the lowest possible return achievable in the game. On the other hand, if we hit the jackpot with the initial roll of 20, our total return will be equal to $ \$20 \times 100= \$2000 $ , the maximum achievable reward in the game. Since each of the faces is equally probable, the expected return from this strategy is equal to

\[\begin{equation*} \sum_{i=1}^{20} \frac{1}{20} \times \$i \times 100 = \$1050 \end{equation*}\]

Without too much thought we can already feel that the strategy of never rolling can be improved upon. For example, given an “unlucky” first roll, trying to roll for a higher number feels reasonable given that the game lasts for 100 rounds which gives plenty of time to compensate for the money not taken early on in the game.

Strategy of Rolling for a High Number

Let us begin by analysing the strategy of rolling the die until we get 20 and only then starting to collect money. Rolling 20 with a twenty-sided die can be viewed as a Bernoulli trial with the probability of success equal to $5\%$. Therefore, the number of rolls needed to get 20 follows the geometric distribution. The expected value of the geometric distribution is equal to $\frac{1}{p}$, where $p$ is the probability of success of the corresponding Bernouilli trial. Thus, the expected number of rolls needed to roll 20 is equal to 20. The expected return from this strategy is then equal to $ \$20 \times (100 - 20)= \$1600 $ (the reason why we subtracted 20 is because we are not getting money in the rounds in which we decide to roll the die). This amount is substantially higher than the return from the strategy of never rolling the die.

However, rolling the die until we get 20 may be too restrictive. Observe that rolling 19 or 20 is twice as likely as rolling just 20 and thus, on average, requires half as many rolls. This increase in probability comes at a cost of only \$0.5 in terms of expected return in rounds where we decide to take money. Therefore, the total expected return of the strategy of rolling until we get 19 or 20 is equal to $\$19.5\times (100 - 10)= \$1755$. The next figure plots the expected return against the lowest number before we stop rolling and start taking money.

Figure 1. Expected Return

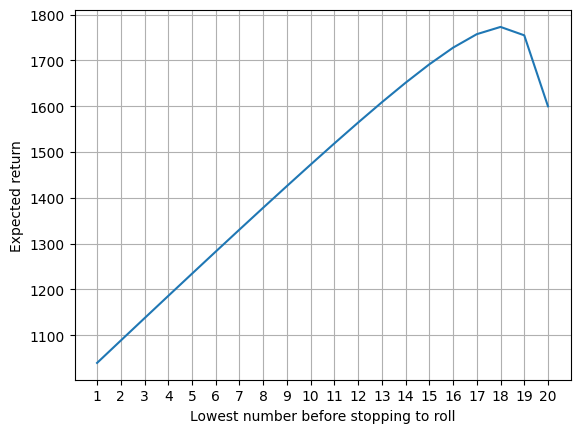
As can be seen from the above plot, there comes a point beyond which it is not optimal to increase the range of numbers to roll for before starting to take money. The graph peaks at 18 with the expected return of \$1773.33. This is pretty good but can we we do any better than this?

Online Strategy

Strategies that require rolling for specific numbers run into the risk of using too many rounds if we start off unlucky. For example, suppose we are rolling for 18, 19 or 20 and have been unlucky to get any of these numbers in the first 10 rolls. The expected number of rolls to get any of these numbers is independent of the previous roll history and thus is equal to $\frac{20}{3}\approx 6.66$. Thus, our expected total reward under the strategy of rolling for 18, 19 and 20, and starting in round 11 is equal to $\$19 \times (90 - \frac{20}{3}) \approx \$1583.33$. This, of course, is considerably less than the expected strategy return at the beginning of the game. Is there a way to improve upon these strategies?

Consider a set of strategies that tell us the optimal decision to make at any given round of the game and for any face of the die that is currently up. Let us call such stategies as “online” strategies (in the sense that they use current information about the state of the game to make a decision). Since such strategies adjust to the way the game is developing, we should expect that they outperform strategies that do not take such information into account, like all the stretegies we have reviewed so far. Let us try to develop such a strategy.

As a reminder, at the start of each round, we have two options: to take money or to roll the die. Therefore, if we can assign values to each of the two options, we can choose the one with the higher value associated with it. How can we assign values to these options? The value of taking money seems straightforward enough - the value is equal to the face of the die that is currently up. What about the value of taking a roll? We can assign value to rolling the die as follows:

\[\begin{equation} V(x, t) = \frac{ | 101 - t - E[G] | \times E[X|X > x]}{101 - t}, \label{eq:1} \end{equation}\]

where

• $X$ is a random variable that takes values in $\{1, 2, …, 20\}$ with equal probability
• $G$ is the geometric random variable with $p=\frac{20}{|\{x+1, x+2, …, 20\}|}$
• $t\in \{1, 2, …, 100\}$ is the current round
• $x\in \{1, 2, …, 20\}$ is the current value of the die
• $V(x, t)$ is the value of rolling the die at the beginning of round $t$ and having $x$ as the current value of the die

Estimating the value of this online strategy is difficult. Therefore, we will use Python to evaluate the strategy in the next subsection.

Python Implementation

We start by loading the required Python libraries.

import pandas as pd
import random

Next we implement roll_value function that implements equation ($\ref{eq:1}$).

def roll_value(x: int, t: int) -> float:
    """
    Return value of rolling a 20-sided die at the start of round t given the current value of the die x.
    
    :param x: current value of the die
    :param t: current round of the game
    :return: roll value
    """
    if x < 20:
        remaining_rounds = (101 - t)
        avg_n_rolls = 20 / (20 - x)
        avg_value = (21 + x) / 2
        return max(remaining_rounds - avg_n_rolls, 0) * avg_value / remaining_rounds
    return 0

Figure 2 below shows how roll values change with the round of game for some values of $x$.

Figure 2. Roll Values

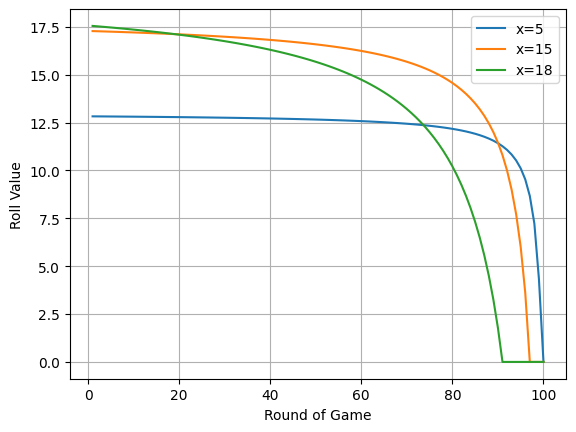
From the above figure we can see that it is never optimal to roll when $x=18$, even at the very start of the game (this is because roll values are below 18 for every round in the game, i.e., taking money in the amount of \$18 will always be the more valuable option). For smaller values of $x$, however, this is no longer true.

To estimate the expected value of our online strategy, we will play the game 100,000 times and inspect the distribution of the earned amounts.

n_games = 100000
rewards_by_game = []
for game in range(n_games):
    reward = 0
    x = random.choice(range(1, 21))
    for t in range(1, 101):
        if roll_value(x, t) > x:
            x = random.choice(range(1, 21))
        else:
            reward += x
    rewards_by_game.append(reward)
    
rewards_by_game = pd.Series(rewards_by_game)
rewards_by_game.describe()

count    100000.000000
mean       1792.096120
std         140.076402
min         580.000000
25%        1728.000000
50%        1800.000000
75%        1900.000000
max        2000.000000
dtype: float64

The average reward is equal to \$1792, which is higher than the reward we achieved by always rolling for 18, 19 or 20.